Bagi sebagian besar pengamat dan praktisi IT khususnya layanan internet, laporan tahunan (
Annual Report) yang dirilis oleh
We are social & Hootsuite - sebuah situs layanan manajemen konten yang menyajikan layanan media
online yang terhubung dengan berbagai situs
social networking seperti Facebook, Youtube, Instagram, Twitter, dll. - selalu dinanti-nantikan.
Kenapa?
Karena
We are social & Hootsuite secara detail menyajikan tren penggunaan internet dan perilaku pengguna internet di seluruh dunia, termasuk Indonesia.
Secara umum konten laporannya terdiri dari:
- Jumlah total populasi, koneksi seluler (mobile), jumlah pengguna internet dan pengguna media sosial aktif
- Tren pertumbuhan digital tahunan
- Kepemilikan perangkat pengguna internet
- Waktu rata-rata harian pengguna internet menggunakan berbagai perangkat
- Dll.
Untuk tahun 2021, We are social & Hootsuite telah merilis laporan hingga bulan Januari 2021 pada minggu kedua Februari 2021.
Berikut beberapa informasi dalam laporan Digital 2021: Indonesia:
Overview Indonesia
- Jumlah populasi penduduk Indonesia (hingga Januari 2021): 274,9 juta
- Koneksi menggunakan seluler (mobile): 345,3 juta
- Jumlah pengguna internet: 202,6 juta
- Jumlah pengguna media sosial yang aktif: 170 juta
Pertumbuhan Digital Tahunan
- Pertumbuhan populasi (Januari 2021 vs Januari 2020): +1,1% (+2,9 juta)
- Pertumbuhan koneksi seluler (mobile): +1,2% (+4 juta)
- Pertumbuhan pengguna internet: +15,5% (27 juta)
- Pertumbuhan pengguna media sosial aktif: +6,3% (10 juta)
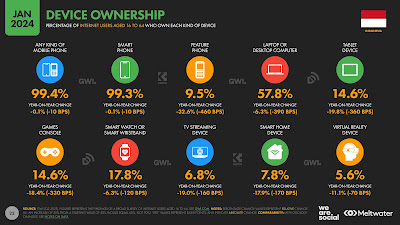
Kepemilikan Perangkat Pengguna Internet
- Telepon seluler (jenis apa pun): 98,3%
- Smartphone: 98,2%
- Telepon seluler bukan smartphone: 16%
- Komputer laptop atau desktop: 74,7%
- Perangkat tablet: 18,5%
- Perangkat TV streaming: 6%
- Konsul Game: 16,2%
- Perangkat smart home: 5,7%
- Perangkat smart watch atau wristband: 13,3%
- Perangkat virtual reality: 4,2%
Waktu Rata-Rata Harian Pengguna Internet Menggunakan Perangkat
Waktu rata-rata harian pengguna internet:
- Menggunakan internet (dari perangkat apa pun): 8 jam 52 menit
- Menonton siaran TV maupun streaming TV: 2 jam 50 menit
- Menggunakan media sosial: 3 jam 14 menit
- Membaca berita online dan koran: 1 jam 38 menit
- Mendengarkan layanan music streaming: 1 jam 30 menit
- Mendengarkan siaran radio: 33 menit
- Mendengarkan layanan podcasts: 44 menit
- Bermain video games menggunakan konsul games: 1 jam 16 menit
Dan masih banyak lagi informasi terkait perilaku pengguna internet di Indonesia.
Jika Anda tertarik dengan laporan We are social & Hootsuite ini, Anda dapat men-download laporan Digital 2021: Global Overview dan Digital 2021: Indonesia pada link di bawah ini.
Disclaimer:
Report Digital 2021 ini di-download dari situs resmi https://datareportal.com/digital-in-indonesia